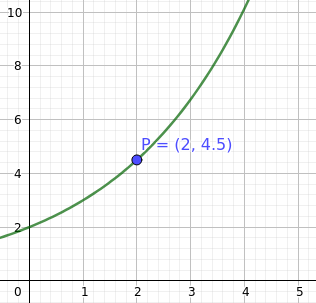
Gegeben ist die Funktion $f(x)=2\cdot 1,5^x$ (siehe Bild). Liegen die Punkte $P(2 | 4,5)$ und $Q(6|20)$ auf dem Graphen von $f$?
Lösung:
Um die Lösung zu berechnen, setzen wir den $x$-Wert der beiden Punkte in $f(x)$ ein und vergleichen das Ergebnis mit dem $y$-Wert.
$$f(2)=2\cdot 1,5^2=4,5$$ $$f(6)=2\cdot 1,5^6\approx 22,78$$
Da $f(2)=4,5$ ist und dieser Wert mit dem $y$-Wert von $P$ übereinstimmt, liegt $P$ auf dem Graphen von $f(x)$. Da $f(6)\approx 22,78$ ist und dieser Wert nicht mit dem $y$-Wert $20$ von $Q$ übereinstimmt, liegt $Q$ nicht auf dem Graphen von $f(x)$.
- S. 206 Nr. 2
Die Lösungen zu den Aufgaben sind gebündelt unten zu finden.
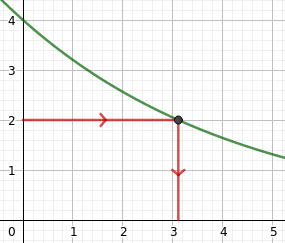
Gegeben ist die Exponentialfunktion $f(x)=4 \cdot 0,8^x$ (siehe Bild). Für welchen Wert von $x$ nimmt die Funktion den Wert $y=2$ an?
Lösung:
Diese Aufgabe kann man als Schnittpunktaufgabe zwischen $f(x)$ und der horizontalen Geraden $g(x)=2$ auffassen. Dementsprechend berechnet man den Wert für $x$ durch Gleichsetzen der Funktionsgleichungen und Auflösen nach $x$.
$$\begin{array}{rcll} f(x) &=& g(x) \\ 4\cdot 0,8^x &=& 2 &|:4\\ 0,8^x &=& 0,5 &|\log_{0,8}(...)\\ x &=& \log_{0,8}(0,5) \\ x &\approx& 3,11 \end{array}$$
Die oben stehende Rechnung zeigt, dass $f(3,11)\approx 2$ gilt.
- S. 206 Nr. 3
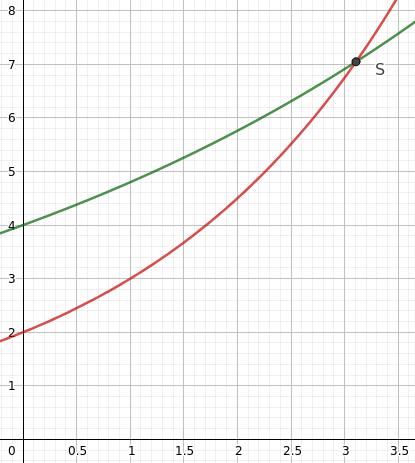
Gegeben sind die Exponentialfunktionen $f(x)=4\cdot 1,2^x$ und $g(x)=2\cdot 1,5^x$ (siehe Bild). Bestimme die Koordinaten des Schnittpunkt S von $f$ und $g$.
Lösung:
Ähnlich wie im Beispiel "Umkehrwerte" setzen wir die Funktionsgleichungen gleich und lösen nach $x$ auf. Anschließend bestimmen wir den $y$-Wert des gesuchten Punkts durch Einsetzen von $x$ in $f$ oder $g$:
$$\begin{array}{rcll} f(x) &= &g(x) \\ 4\cdot 1,2^x &= &2\cdot 1,5^x &|:2, :(1,2^x)\\ \frac{4}{2} &= &\frac{1,5^x}{1,2^x} &|TU (Pot. Ges.)\\ 2 &= &\left(\frac{1,5}{1,2}\right)^x &|TU\\ 2 &= &1,25^x &|\log_{1,25}(...)\\ \log_{1,25}(2) &= &x\\ 3,11 &\approx&x \end{array}$$
Setzen wir nun $x$ in $f(x)$ ein, erhalten wir $f(3,11)\approx7,05$ als $y$-Wert des Schnittpunkts. Somit hat S die Koordinaten $(3,11|7,05)$.
- S. 206 Nr. 4
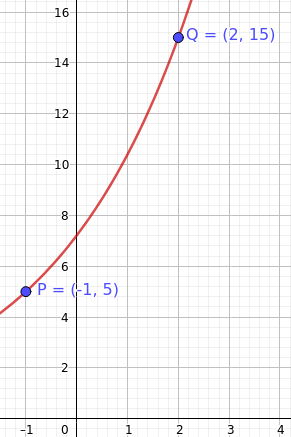
Gegeben sind die Punkte $P(-1|5)$ und $Q(2|15)$. Bestimme eine Exponentialfunktion der Form $f(x)=a\cdot b^x$ mit $a>0$, deren Graph durch $P$ und $Q$ verläuft.
Lösung:
Als Ansatz haben wir die Funktionsgleichung $f(x)=a\cdot b^x$ gegeben. Als bekannte Informationen verwenden wir die beiden Punkte:
- $P(-1|5)$ bedeutet, dass $f(-1)=5$ sein soll. Also gilt $a\cdot b^{-1}=5$.
- $Q(2|15)$ bedeutet, dass $f(2)=15$ sein soll. Also gilt $a\cdot b^{2}=15$.
Die erste Gleichung können wir nach $a$ auflösen:
$$\begin{array}{rcl} a\cdot b^{-1} &=&5 \\ a\cdot\frac{1}{b} &=&5 \\ a &=&5\cdot b \end{array}$$
Diesen Term für $a$ können wir in die zweite Gleichung einsetzen:
$$\begin{array}{rcl} a\cdot b^2 &=&15 \\ 5\cdot b\cdot b^2 &=&15 \\ 5\cdot b^3 &=&15 \\ b^3 &=&3 \\ b &=&\sqrt[3]{3}\approx 1,44 \end{array}$$
Diesen Wert für $b$ können wir nun in den ersten Term für $a$ einsetzen und erhalten $a=5\cdot b=5\cdot\sqrt[3]{3}\approx 7,2$.
Somit ist unsere gesuchte Funktionsgleichung $f(x)=7,2\cdot 1,44^x$.
- S. 206 Nr. 5
- S. 206 Nr. 6, 8
$1 cm^3$ Kuhmilch enthielt $2$ Stunden nach dem Melken $9000$ Keime; $1$ Stunde später waren $32000$ Keime vorhanden.
- Wie viele Keime befanden sich am Anfang in $1 cm^3$ frisch gemolkener Milch, wenn man exponentielles Wachstum annimmt?
- Ein kritischer Wert an Keimen ist bei einer Konzentration von $100.000$ Keimen pro $cm^3$ erreicht. Wie lange dauert es, bis diese Konzentration erreicht ist?
- Lösung für Übung - Kuhmilch
- Rekonstruktion mit $P(2|9000)$ und $Q(3|32000)$, $f(x)\approx 712\cdot(\frac{32}{9})^x$, also Anfangswert ca. $712$ Keime
- Ansatz $f(x)=100000 ~\Rightarrow~ x=\log_{\frac{32}{9}}(\frac{100000}{712})\approx 3,9$, also nach $3,9h$
