 Ein Schachbrett hat $8\cdot 8=64$ Felder. Es wird also 64 mal verdoppelt!
Ein Schachbrett hat $8\cdot 8=64$ Felder. Es wird also 64 mal verdoppelt!
 Der Weltrekord im Falten von (Klo-)Papier liegt nur bei 13 Faltungen!
Der Weltrekord im Falten von (Klo-)Papier liegt nur bei 13 Faltungen!
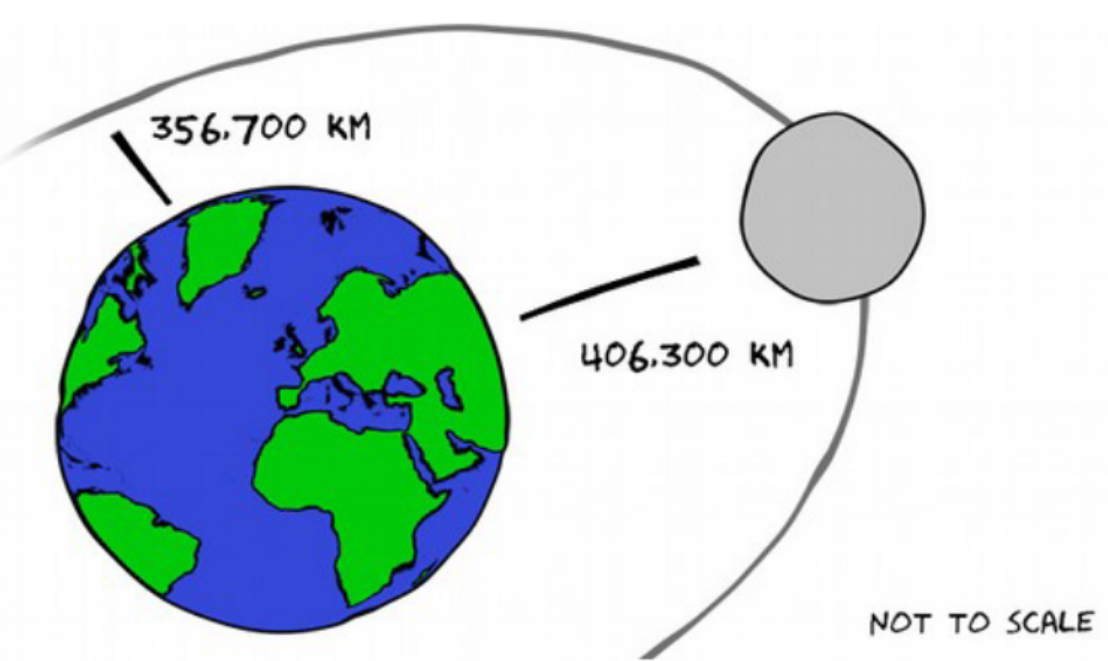 Die Entfernung von der Erdezum Mond beträgt imDurchschnitt 384.402km
Die Entfernung von der Erdezum Mond beträgt imDurchschnitt 384.402km
a) Versucht eine Formel zu erstellen, mit der die Anzahl der Reiskörner auf dem $x$-ten Feld [die Dicke des Papiers nach der $x$-ten Faltung] berechnet werden kann! Tipp: Erstellt zunächst eine Wertetabelle!
b) Schaut euch danach das Video rechts an.
Ist die Basis $b>1$, so spricht man von exponentiellem Wachstum, ist $0<b<1$, spricht man von exponentiellem Zerfall.
Ähnlich wie bei quadratischen Funktionen oder Polynomen gibt es auch hier eine Normalform, mit deren Hilfe man Verschiebungen, Streckungen und Stauchungen ablesen bzw. erzeugen kann:
$$f(x)=a\cdot b^{(x-c)}+d$$
Versucht mit dem Geogebra-Applet unten herauszufinden:
- Was passiert, wenn du die Basis $b$ veränderst?
- Wofür steht der Parameter $a$?
- Wofür stehen die Parameter $c$ und $d$?
Achtet auf besondere Punkte im Graphen (Nullstellen, y-Achsenabschnitte, etc) und Verschiebungen, Streckungen, Stauchungen im Vergleich zur blauen Funktion $2^x$. Notiert eure Beobachtungen.
- Der Parameter $a$ ist der Anfangswert (oder y-Achsenabschnitt) der Exponentialfunktion.
- Der Parameter $b$ ist die Basis der Exponentialfunktion.
- Es muss $b>0$ gelten, da sonst die Funktion nicht gezeichnet werden kann.
- Gilt $0<b<1$, so spricht man von Zerfall, z.B. bei $f(x)=0.75^x$ oder $g(x)=\frac{1}{3}^x$
- Gilt $b>1$, spricht man von Wachstum, z.B. bei $h(x)=2^x$ oder $i(x)=1.17^x$.
- Der Parameter $c$ ist die Verschiebung entlang der x-Achse.
- Der Parameter $d$ ist die Verschiebung entlang der y-Achse.
Tipp: Du kannst mit dem obigen GeoGebra-Applet ausprobieren, welcher Graph zu welcher Gleichung passt.
Tipp 2: Es bleibt ein Graph und eine Funktionsgleichung übrig!
