Wiki: Mathe und Info

Verschiebung und Streckung der Normalparabel

Was ist eine quadratische Funktion?

Eine Funktion mit der Gleichung $f(x) = ax^2 + bx + c$ wird quadratische Funktion genannt. Der Graph einer beliebigen quadratischen Funktion, den man auch als Parabel bezeichnet, lässt sich durch Verschiebungen und Streckungen der Normalparabel gewinnen.

Aufgbabe 1 - Verschiebungen und Streckung der Normalparabel

Untersuche mit dem GeoGebra-Applet, durch welchen Parameter welche Verschiebung oder Streckung hervorgerufen wird. Hierfür verschiebst du den Schieberegler in der GeoGebraApp, um für die einzelne Parameter konkrete Werte einzusetzen. Unten findest du Hinweise zur Benutzung von GeoGebra. Du kannst das GeoGebra-Applet nehmen, das du hier neben siehst oder die reguläre GeoGebra-App (Grafikrechner). Halte deine Ergebnisse in der Tabelle des Vordrucks fest.

Beschreibe den Zusammenhang zwischen den Parametern $d$ bzw. $c$ und dem Scheitelpunkt der Parabeln aus dem ersten Teil der Aufgabe.

Geogebra Applet

Hilfe GeoGebra allgemein

Geogebra besteht aus zwei Hauptteilen.

Die obere Hälfte des Bildschirms nimmt ein Koordinatensystem ein.
- Hier werden die Graphen der Funktionen angezeigt, die ihr eingegeben habt.
- Mit den beiden Lupen-Symbolen am rechten Rand könnt ihr das Bild vergrößern und verkleinern.
- Mit dem Symbol mit den drei Balken oben links kommt ihr in ein Menü, in dem ihr die Datei speichern oder eine neue Datei anlegen könnt.

Auf der unteren Hälfte findet ihr die Eingabezeile und die Tastatur. GeoGebra benutzt eine spezielle, mathematische Tastatur, die aus mehreren Bereichen besteht.
- Zahlen und Operatoren
- vorgefertigte mathematische Funktionen
- Buchstaben
- griechische Buchstaben

Hilfe zu Aufgabe 1

Um Aufgabe 1 zu lösen, müsst ihr zunächst die Funktion $f(x) = a \cdot x^2$ eingeben.

Das „f“ und das „a“ findet ihr auf der „Buchstaben“-Tastatur, alles andere auf der „Zahlen und Operatoren“-Tastatur.
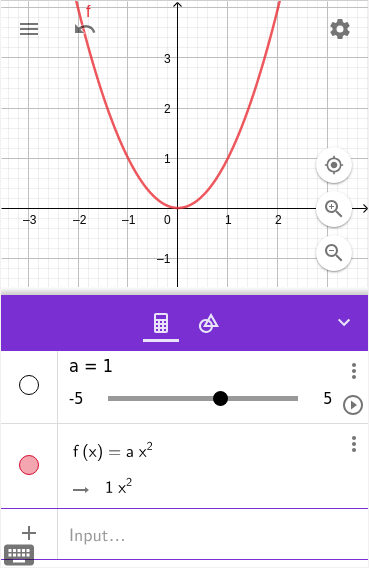
Anschließend sollte eure App so aussehen wie links.
- Im Koordinatensystem seht ihr den Graphen zu eurer Funktion.
- In der ersten Zeile unten wurde ein Schieberegler erstellt, der den Wert von Parameter $a$ verändert.
- In der zweiten Zeile unten seht ihr die eingegebene Funktionsgleichung.
Ihr könnt nun mit dem Schieberegler den Parameter $a$ verändern und damit auch die Funktion $f$.
Nun könnt ihr die Aufgabe bearbeiten!
Bevor ihr die nächste Darstellungverwendet, erstellt bitte ein neues Dokument.

Lösung zu Aufgabe 1

Lösung (PDF)

Definition "quadratische Funktion" bzw. "Normalform"

Eine Funktion $f$ mit der Funktionsgleichung in der Normalform $f(x)=a \cdot x^2 + b \cdot x + c$ nennt man quadratische Funktion.

Der Graph einer linearen Funktion ist eine Parabel.
Der Parameter $a$ heißt Streckfaktor von $f$.
- Ist $a=1$, so ist $f$ die Normalparabel.
- Ist $a>0$, so ist $f$ nach oben geöffnet (Fig. 1, grün).
- Ist $a<0$, so ist $f$ nach unten geöffnet (Fig. 1, rot).
- Ist $|a|<1$, so ist $f$ in y-Richtung gestaucht (Fig. 2).
- Ist $|a|>1$, so ist $f$ in y-Richtung gestreckt (Fig. 3).
Der Parameter $c$ ist der y-Achsenabschnitt von $f$.

Fig. 1: positive/negative Parabel

Fig. 2: gestauchte Parabeln

Fig. 3: gestreckte Parabeln

Aufgabe 2 - Nach oben oder unten geöffnet?

Aufgabe 3 - Parabel zeichnen

Zeichne die folgenden Parabeln in dein Heft:

$g(x) = (x + 4)^2$
$h(x) = 2x^2$

Verschiebe/strecke/stauche die Parabeln gedanklich und notiere hier die daraus resultierenden Funktionsgleichungen.

	Aktion	neue Funktionsgleichung
$g(x)$	Stauchung um $\frac{1}{2}$ Verschiebung um $\pi$ Einheiten nach rechts Verschiebung um 2 Einheiten nach unten
$h(x)$	Streckung um Faktor 7 Verschiebung nach rechts um 2 Einheiten Verschiebung nach unten um 2 Einheiten