Strahlensatz

Was sind Strahlensätze?¹⁾

Die Strahlensätze sind direkte Folgerungen aus der zentrischen Streckung. Grundsätzlich lassen sich die Strahlensätze bei zwei Arten von Figuren anwenden, bei sogenannten "V−Figuren" und "X−Figuren".

Voraussetzungen²⁾

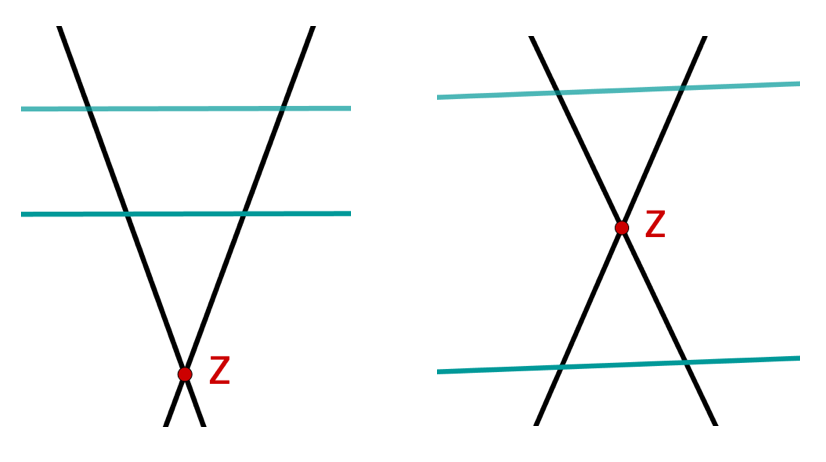
Um die Strahlensätze anzuwenden, müssen drei Voraussetzungen erfüllt sein:

richtig

falsch

Zwei Geraden $g$ und $h$, die sich in einem Punkt $Z$ schneiden.

Diese beiden werden von zwei parallelen Geraden geschnitten.

Wobei keine der beiden parallelen Geraden durch den Schnittpunkt der ersten beiden Geraden geht.

Aussage³⁾

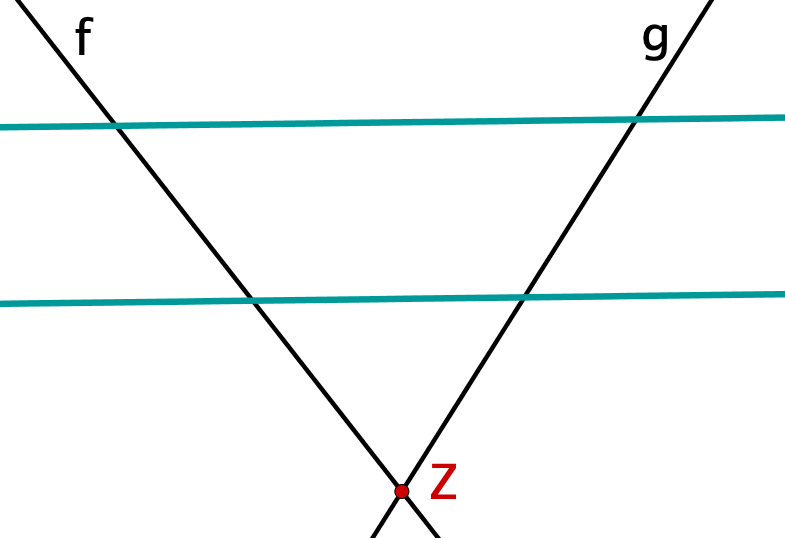
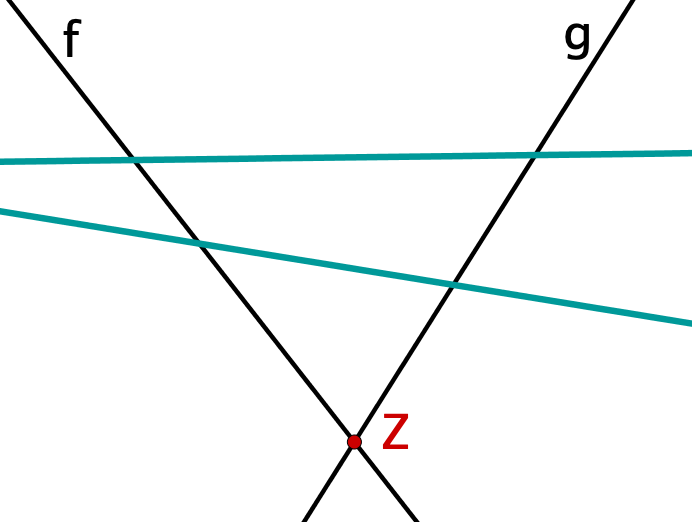
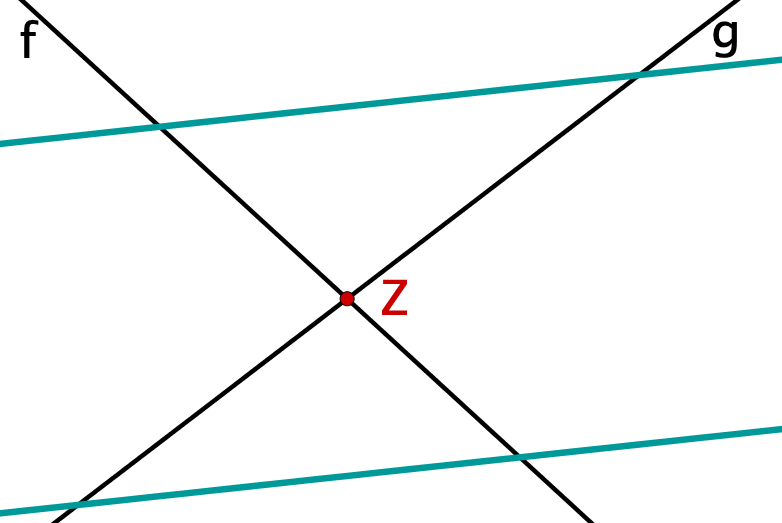
Wenn die oben genannten Voraussetzungen erfüllt sind, dann gelten folgende Aussagen:

V-Figur

X-Figur

Für beide Figuren gelten die folgenden beiden Strahlensätze.

1. Strahlensatz⁴⁾

$\frac{\overline{ZA'}}{\overline{ZA}} = \frac{\overline{ZB'}}{\overline{ZB}}$

und

$\frac{\overline{AA'}}{\overline{ZA}} = \frac{\overline{BB'}}{\overline{ZB}}$

2. Strahlensatz⁵⁾

$\frac{\overline{ZA'}}{\overline{ZA}} =\frac{\overline{B'A'}}{\overline{BA}}$

oder

$\frac{\overline{ZB'}}{\overline{ZB}} = \frac{\overline{B'A'}}{\overline{BA}}$

1. Strahlensatz - Ausführliche Erklärung (Lehrerschmidt)

2. Strahlensatz - einfach erklärt (Lehrerschmidt)

Strahlensätze interaktiv

Aufgaben zu den Grundlagen

Aufgaben serlo.org
- Nr. 3
- Nr. 5
- Nr. 6
- Nr. 4
- Nr. 7
- Nr. 8
- Nr. 9
- Nr. 10 (Sternchenaufgabe)

Bitte in dieser Reihenfolge!

Anwendung der Strahlensätze - Baumhöhe bestimmen

Eigene Messung durchführen

Messt mit Hilfe der hier beschriebenen Methode eine unzugängliche Höhe, z.B. euer Haus oder einen hohen Baum.
Dokumentiert eure Messung anhand einer Bilderserie oder eines Videos.
Erstellt eine Skizze, die eure Strahlensatzfigur zur Messung enthält. Stellt dort die entsprechenden Formeln der Längenverhältnisse dar.

Baumhöhe messen - Beispielvideo

Anwendungsaufgaben

S. 196
- Nr. 25
- Nr. 26

Lösungen bitte hier hochladen.

Umkehrung der Strahlensätze

Bei den Strahlensätzen gilt die Umkehrung nur in einigen Fällen, nicht aber in allen.

1. Strahlensatz

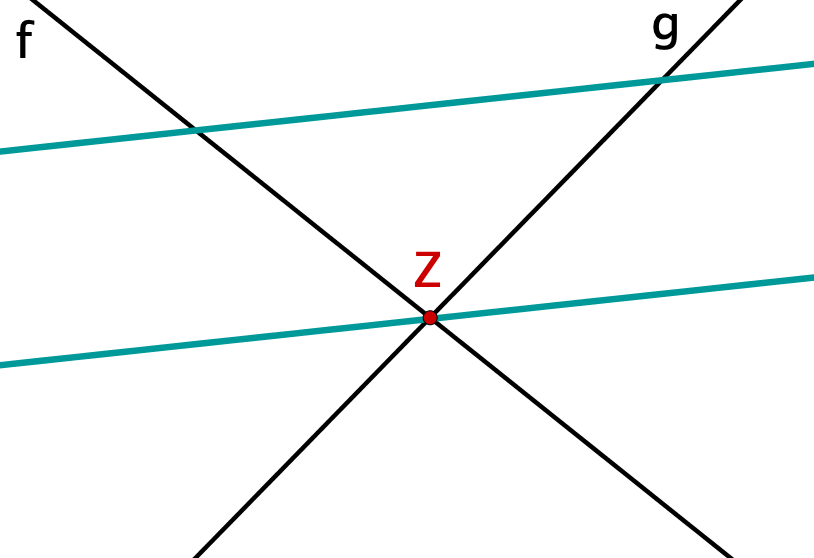
Wenn sich zwei Halbgeraden $a$ und $b$ in einem Punkt $Z$ schneiden und es gibt weiterhin zwei Geraden $g$ und $h$, welche die Geraden $a$ und $b$ in den Punkten $A_1$, $A_2$ sowie $B_1$ und $B_2$ schneiden, dann gilt folgende Schlussfolgerung:

$$\frac{\overline{SA_1}}{\overline{SA_2}} = \frac{\overline{SB_1}}{\overline{SB_2}} \Rightarrow g || h$$

Aus dem gleichen Seitenverhältnis folgt also die Parallelität.

Übungen

S. 199
- Nr. 3
- Nr. 4

¹⁾ , ²⁾ , ³⁾ , ⁴⁾ , ⁵⁾

Quelle: serlo.org unter CC BY-SA