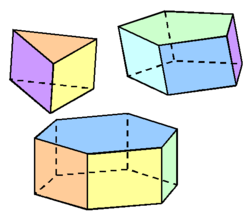
Diese Geschenkschachtel hat ungefähr die Form eines Primas mit einem regulären Sechseck als Grundfläche.

Mit der Vorderfront als "Grundfläche" ist solch ein Gewächshaus annähernd ein Prisma.
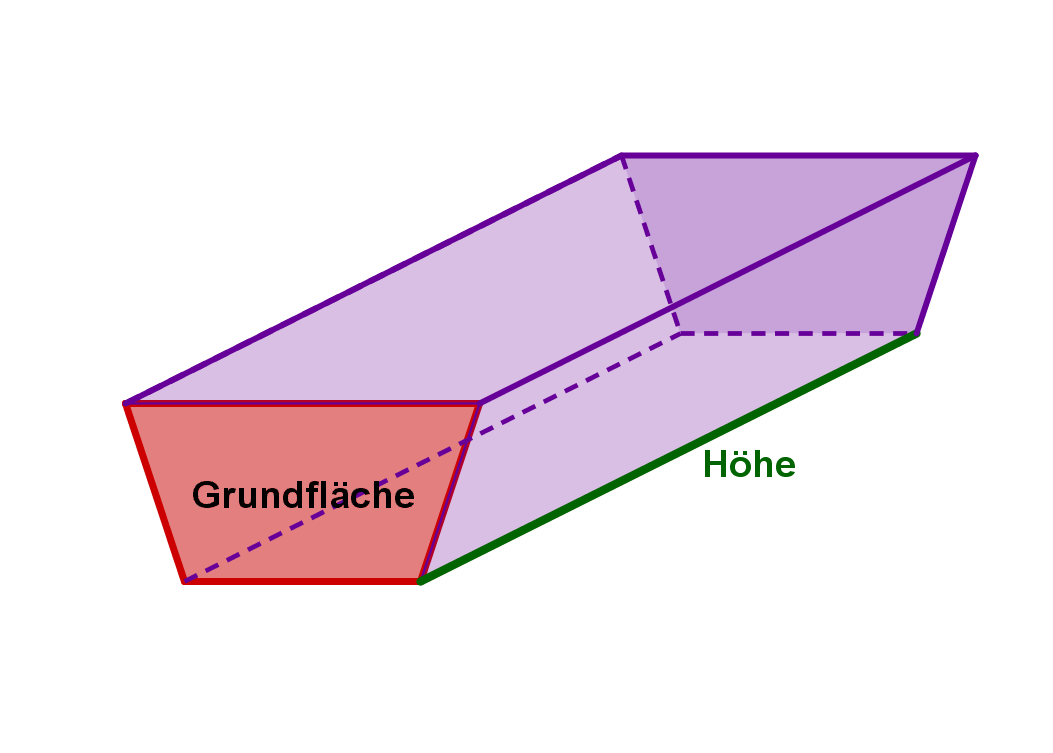
Grundfläche
Bemerkung: Auch wenn es "Grundfläche" heißt, muss die Grundfläche nicht unbedingt unten sein. Ein Prisma kann auch auf einer der Seitenflächen liegen.
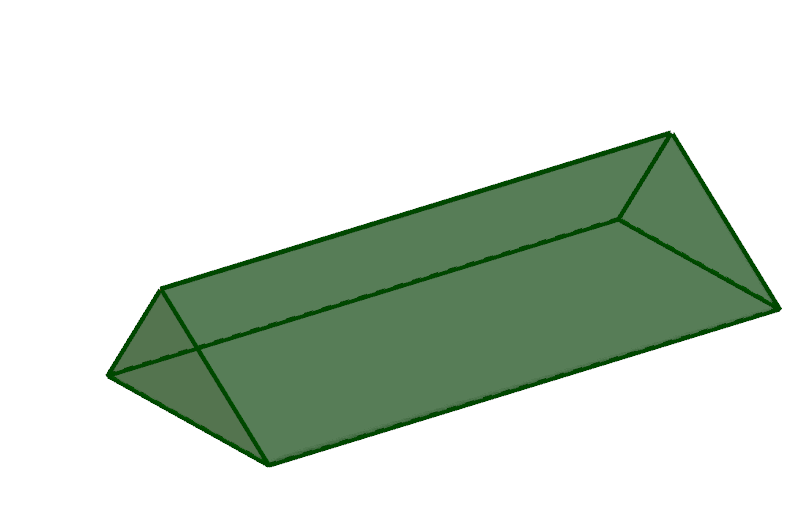
Liegendes Prisma mit dreieckiger Grundfläche
Höhe
Die Höhe eines Prismas ist der Abstand zwischen der Ebene, in der die Grundfläche des Prismas liegt zu der Ebene, in der die (der Grundfläche gegenüber liegende) Deckfläche liegt.

Um das Thema Prismen sinnvoll abzurunden bietet es sich an, dass du dein Wissen anhand mehrerer Aufgaben testest. Um deine Lösungen für dich in Zukunft nachvollziehbar zu machen, besteht die Aufgabe hier neben der Rechnung darin, eine Aufgabe in Form eines Erklärvideos zu erläutern. Dazu kannst du eins Handykamera oder ein Tablet verwenden.
- Löse alle Aufgaben der S. 181
- Erstelle ein Video, wie du eine der Aufgaben löst. Achte bei der Erstellung des Videos auf die Bewertungskriterien für Erklärvideos (ganz unten auf der Seite)
- Die Zeichnungen in Nr. 1 und Nr. 4 können weggelassen werden.
- Nachfolgend ist pro Aufgabe aufgelistet, was ins Video soll bzw. nicht ins Video soll:
- Nr. 1: 2 Teilaufgaben
- Nr. 2: eine Teilaufgabe außer a)
- Nr. 3: eine Teilaufgabe außer a)
- Nr. 4: c) und d) müssen ins Video
- Nr. 5: eine Teilaufgabe deiner Wahl
- Nr. 6: eine Teilaufgabe deiner Wahl
- Wenn du während der Bearbeitung dieser Aufgabe Fragen hast, wende dich bitte an mich.
| Technische Aspekte | 2 Punkte |
|---|---|
| Bild/Kamera | |
| Ton/Verständlichkeit | |
| Inhaltliche Aufteilung | |
| Einleitung und Begrüßung/Anmoderation vorhanden | 0,5 |
| Sachlogische Gliederung/Struktur/Reihenfolge erkennbar | 1 |
| Einzelne Szenen mit Überschriften/Beschilderung versehen | 1 |
| Inhalte vollständig und fachlich korrekt vorgetragen | 4 |
| Fachsprache korrekt verwendet | 1 |
| Verabschiedung/Schlussmoderation vorhanden | 0,5 |
| Gestaltung/Originalität | 3 Punkte |
| Karten | |
| Design | |
| Bilder | |
| Farben | |
| Übersichtlichkeit | |
| sonstiges | |
| Summe $\Sigma$ |
In dieser Aufgabe geht es darum, dass du dir das Thema Prismen einmal in der Praxis anschaust. Hierzu werden wir uns eine Verpackung einmal ganz genau anschauen. Zu dieser Verpackung erstellst du am Ende der Aufgabe eine Ausarbeitung. Das Medium kannst du dabei aus verschiedenen Optionen wählen.
- Organisiere dir eine Verpackung, die du nicht mehr brauchst. Diese Verpackung muss dabei die Form eines Prismas haben.
- Halte das Aussehen deiner Verpackung in Form von Bildern fest. Achte hier auf verschiedene Blickwinkel und dass alle Aspekte des Prismas zu erkennen sind. Erläutere bei den Bildern auch kurz diese Eigenschaften.
- Zeichne zwei unterschiedliche Netze zu deinem Prisma. Achte dabei darauf, dass die Verhältnisse ungefähr stimmen.
- Miss dein Prisma aus und trage die Daten in eines deiner Netze ein.
- Berechne die Oberfläche und das Volumen deines Prismas.
- Überlege dir, warum mehr Pappe für die Verpackung benötigt wird als die bloße Oberfläche des Prismas einnimmt. Überlege außerdem, warum das Volumen des Inhaltes der Verpackung (z.B. Toblerone-Schokolade) in der Regel nicht dem gesamten Volumen der Verpackung ensptricht.
Erstelle aus deinen Rechnungen eines der folgenden Produkte:
- Präsentation (PowerPoint, LibreOffice Presenter, GoodNotes etc.)
- Textdokument (Word, LibreOffice Writer etc.)
- Video (Bewertungskriterien s.o.)
Das Ergebnis wird benotet. Wenn du während der Bearbeitung Fragen hast, stelle sie mir gerne 
Abgabefrist ist Dienstag, 30.03.21 - 13:00 Uhr
| Gesamteindruck | 2 Punkte |
|---|---|
| Einheitliches Layout | |
| Übersichtliche Gestaltung | |
| Inhaltliche Aufteilung | |
| Titelseite | 0,5 |
| Sachlogische Gliederung/Struktur/Reihenfolge erkennbar | 1 |
| Einzelne Abschnitte mit Überschriften versehen | 1 |
| Inhalte vollständig und fachlich korrekt dokumentiert | 4 |
| Fachbegriffe korrekt verwendet | 1 |
| Abschluss / Fazit vorhanden | 0,5 |
| Gestaltung/Originalität | 3 Punkte |
| Symbole | |
| Design | |
| Bilder | |
| Farben | |
| sonstiges | |
| Summe $\Sigma$ |