Ein Lineares Gleichungssystem (LGS) besteht aus linearen Gleichungen. Im Folgenden ist z.B. ein $4\times 3$-LGS sowie die zugehörige Lösungsmenge dargestellt:
$$\begin{array}{l|rrrcr|} \bbox[yellow,2px,border:1px dotted]{I.} & \bbox[magenta,2px,border:1px dotted]{-4}\cdot\bbox[lime,2px,border:1px dotted]{a} & \bbox[magenta,2px,border:1px dotted]{+3}\cdot\bbox[lime,2px,border:1px dotted]{b} & \bbox[magenta,2px,border:1px dotted]{-1}\cdot\bbox[lime,2px,border:1px dotted]{c} &=& \bbox[magenta,2px,border:1px dotted]{7} \\ \bbox[yellow,2px,border:1px dotted]{II.} & 8a & -6b & +2c &=& -14 \\ \bbox[yellow,2px,border:1px dotted]{III.} & & 1b & +2c &=& 3 \\ \bbox[yellow,2px,border:1px dotted]{IV.} & -5a & & -3c &=& 4 \\ \end{array}$$ $$\mathbb{L}=\left\{a=-\frac{33}{23};b=\frac{17}{23};c=\frac{26}{23}\right\}=\left\{\left(-\frac{33}{23};\frac{17}{23};\frac{26}{23}\right)\right\}$$
- Jedes LGS besteht aus $\bbox[yellow,2px,border:1px dotted]{\bf \text{Gleichungen}}$, die oft mit römischen Zahlen gekennzeichnet sind.
- Jede Gleichung in einem LGS besteht aus $\bbox[lime,2px,border:1px dotted]{\bf\text{Variablen}}$ (z.B. $a,b,c$ oder $x,y,z$ oder $x_1,x_2,x_3,x_4,x_i...$) und $\bbox[magenta,2px,border:1px dotted]{\bf\text{Koeffizienten}}$ (die Zahlen samt Vorzeichen, mit denen die Variablen multipliziert werden).
- Jede Gleichung besteht aus einer linken Seite mit Variablen und Koeffizienten sowie einer rechten Seite mit nur einem Koeffizienten, getrennt durch das Gleichheitszeichen.
- Jedes LGS hat eine Lösungsmenge $\mathbb{L}$, die Werte für die Variablen enthält, sodass jede Gleichung gelöst wird.
- Diese Lösungsmenge besteht oft aus genau einem Lösungsvektor, manchmal aber auch aus unendlich vielen oder gar keinem (hierzu später mehr).
$$\begin{array}{l}\text{I}\\\text{II}\end{array}\left|\begin{array}{c} 1a + 2b = 3\\ 4a + 5b = 6 \end{array}\right|$$
(2) Im zweiten Schritt können wir die beiden Gleichungen $I$ und $II$ addieren, um die Variable $a$ zu eliminieren. Hierzu wird für jedes Koeffizientenpärchen addiert, sodass eine neue Gleichung entsteht. Die alte Gleichung $II$ ersetzen wir durch diese neue Gleichung.
$$\begin{array}{crcl} &-3b&=&-6\\ \Rightarrow&b&=&2 \end{array}$$
(4) Da wir nun die Lösung für $b$ kennen, können wir diesen Wert in die Gleichung $I$ einsetzen, um anschließend die Lösung für $a$ zu berechnen:
$$\begin{array}{crcl} &−4a−8b&=&−12\\ \Rightarrow&-4a-8\cdot2&=&-12\\ \Rightarrow&-4a-16&=&-12\\ \Rightarrow&-4a&=&4\\ \Rightarrow&a&=&-1\\ \end{array}$$
(5) Nun haben wir für beide Variablen eine Lösung gefunden. Diese wird als Lösungsmenge aufgeschrieben:
$$\mathbb{L}=\left\{(-1;2)\right\}$$
Wie oben in der Rechnung gesehen, können wir mit dem Additionsverfahren verschiedene Umformungen vornehmen, z.B. eine Gleichung mit einer Zahl zu multiplizieren, oder eine Gleichung mit einer anderen addieren. Insgesamt gibt es diese drei Äquivalenzumformungen:
- Das Vertauschen von zwei Gleichungen
- Das Multiplizieren einer Gleichung mit einer rellen Zahl außer 0
- Das Addieren von zwei Gleichungen
Ein Gleichungssystem mit zwei Gleichungen und zwei Variablen kann man auch als zwei Geraden interpretieren, indem man beide Gleichungen nach y umstellt:
$$\begin{array}{l}\text{I}\\\text{II}\end{array}\left|\begin{array}{c} 1x + 2y = 3\\ 4x + 5y = 6 \end{array}\right|~~\Rightarrow~~\begin{array}{l}\text{I}\\\text{II}\end{array}\left|\begin{array}{c} y = -\frac{1}{2}x + \frac{3}{2}\\ y= -\frac{4}{5}x + \frac{6}{5} \end{array}\right|$$
Diese beiden umgestellten Gleichungen kann man nun als Funktionsvorschrift einer linearen Funktion interpretieren. Beide Geraden schneiden sich in einem Punkt, nämlich genau im oben bereits bestimmten Lösungsvektor $\mathbb{L}=\left\{(-1;2)\right\}$, also im Punkt $(-1|2)$:
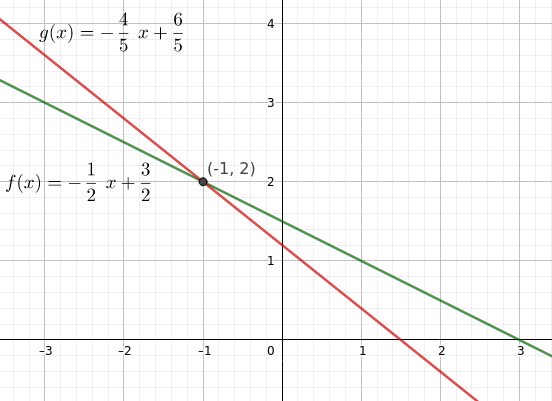
Aus diesem Sachzusammenhang lassen sich Rückschlüsse ziehen, welche verschiedenen Lösungsmöglichkeiten wir für $(2\times2)$-LGS haben:
Zwei Geraden mit genau einem Schnittpunkt:
$$\begin{array}{l}\text{I}\\\text{II}\end{array}\left|\begin{array}{c} -1x + 2y = 2\\ 2x + 3y = 9 \end{array}\right|$$
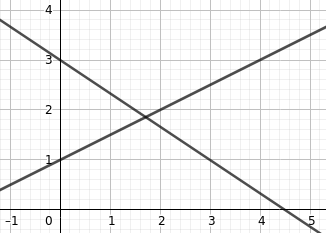
Die Lösungsmenge enthält nur den Schnittpunkt: $$\mathbb{L}=\left\{\left(\frac{12}{7};\frac{13}{7}\right)\right\}$$
Zwei parallele Geraden:
$$\begin{array}{l}\text{I}\\\text{II}\end{array}\left|\begin{array}{c} 4x + 6y = 2\\ 2x + 3y = 9 \end{array}\right|$$
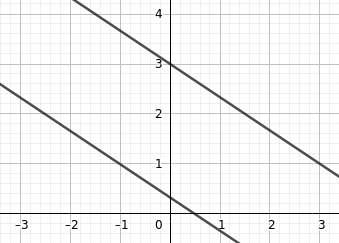
Die Lösungsmenge ist leer: $$\mathbb{L}=\left\{\right\}$$
Zwei identische Geraden:
$$\begin{array}{l}\text{I}\\\text{II}\end{array}\left|\begin{array}{c} 4x + 6y = 18\\ 2x + 3y = 9 \end{array}\right|$$

Die Lösungsmenge enthält unendlich viele Paare für $x$ und $y$, die dieses Gleichungssystem erfüllen.
Die Gleichungssysteme soll mit Hilfe des Additionsverfahrens auf Lösbarkeit untersucht werden:
a) $~~\begin{array}{|rrcl|}2x&-2y&=&-3\\-3x&+3y&=&9\end{array}~~$ b) $~~\begin{array}{|rrcl|}8a&+4b&=&16\\-6a&-3b&=&-12\end{array}$
Die Gleichung $II$ ist für keine Kombination von Werten für $x$ und $y$ lösbar, da sie vereinfacht $0=9$ lautet. Dies stellt einen Widerspruch dar. Somit ist die Lösungsmenge
$$\mathbb{L}=\left\{\right\}$$
Die Gleichung $II$ ist für jede Kombination von Werten für $x$ und $y$ lösbar, da sie vereinfacht $0=0$ lautet. Um die Lösungsmenge zu bestimmen, wählt man eine der beiden Variablen, z.B. $a$ und löst eine der Gleichungen nach der anderen Variablen $b$ auf. Somit erhält man $b=-2a+4$. Somit ist die Lösungsmenge
$$\mathbb{L}=\left\{\left(a;-2a+4\right)|a\in\mathbb{R}\right\}$$
