Potenzfunktionen & Polynome

Potenzfunktionen

Graph Dance

Definition "Potenzfunktion"

Eine Funktion $f$ mit der Funktionsgleichung in der Form $f(x)=a \cdot x^n$ mit $n \in \mathbb{N}$ nennt man Potenzfunktion.

Beispiele:

$f(x) = 3x^2$
$g(x) = \frac{2}{3}x^6$
$h(x) = -7x^4$

Aufgabe 1 - Wertetabelle

In der abgebildeten Wertetabelle sind Potenzfunktionen vom Grad zwei bis Grad sechs, das bedeutet, dass der Exponent zwischen den Werten 1 und 6 liegt.

Bevor du die Wertetabelle ausfüllst, stelle Vermutungen zu den Potenzfunktionen auf, indem du die folgenden Fragen beantwortest:
- In welchen Einträgen der Tabelle werden negative Zahlen stehen?
- In welchen Einträgen der Tabelle werden positive Zahlen stehen?
- In welchen Spalten sind alle Einträge gleich?
- In welchem Eintrag wird die größte, in welchem die kleinste Zahl stehen?
Fülle die Tabelle aus.
Punkt- und Achsensymmetrie sind Eigenschaften aus der Geometrie, die sich auf Funktionen übertragen lassen. Beschreibe, welche Potenzfunktionen punkt- und welche achsensymmetrisch sind. Begründe mit der Wertetabelle.

Wertetabelle

	$a$	$-2$	$-1$	$-0,5$	$-0,25$	$0$	$0,25$	$0,5$	$1$	$2$	$3$
$f$
$f(x)=x$
$f(x)=x^2$
$f(x)=x^3$
$f(x)=x^4$
$f(x)=x^5$
$f(x)=x^6$

Aufgabe 2 - Beautiful Dance Moves

Das Aussehen von Potenzfunktionen kann man mit den Armen nachstellen. In dem Bild rechts (Quelle: http://pixabay.com) könnte eine Potenzfunktion der Art $f(x) = x^2$ dargestellt sein. Führt die folgenden Choreographien durch und überprüft die Bewegung mit Hilfe von GeoGebra:

$x^2$, $x^4$, $x^6$, $x^8$
$x^3$, $x^2$, $x^3$, $x^2$
$x^{100}$, $x^2$, $x^{100}$, $x^2$
$-x^2$, $x^2$, $x$, $-x$, $x^3$, $-x^3$

Überlegt euch in Kleingruppen selbst eine Choreographie. Sucht euch dazu ein kurzes Musikstück aus. Probt die Choreographie. Im Anschluss führt ihr die Choreographie vor. Ziel ist es, dass der Rest des Kurses möglichst viele Potenzfunktionen erkennt.

Aufgabe 3

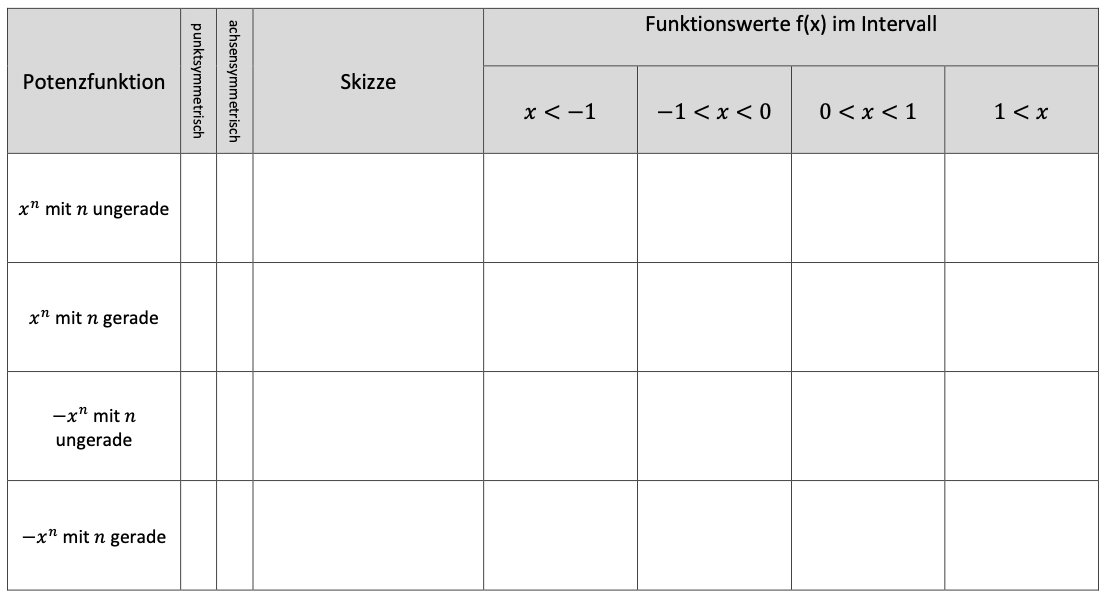
Beschreibe das Aussehen von Potenzfunktionen $f(x)= \pm a x^n$ allgemein. Fertige auch jeweils eine Skizze an und beschreibe wie sich der Graph mit wachsendem $n$ sowohl in negativer als auch positiver Richtung verändert.

Überlege für das Symmetrieverhalten, welche Regelmäßigkeit in Bezug auf die Exponenten du dabei erkennen kannst. Interessant ist hierbei Achsen- und Punktsymmetrie.

Tabelle zu Aufgabe 3

Aufgabe 4

Formuliere einen Merksatz zum Verlauf der Graphen von Potenzfunktionen. Verwende dabei die Fachbegriffe wie z.B. Exponent, Vorfaktor sowie die Namen der Quadranten.

Merksatz - Verlauf der Graphen

Aufgabe 5

Formuliere einen Merksatz zur Symmetrie von Potenzfunktionen. Verwende dabei die unter anderem die folgenden Fachbegriffe:

Achsensymmetrie
Punktsymmetrie
$f(x)$

Merksatz - Symmetrie

Übung 1 - Potenzfunktionen zuordnen

Übung 2 - Aufgabe Schulbuch

Bearbeite folgende Schulbuchaufgabe:

S. 47 Nr. 1

Potenzfunktionen mit negativen Exponenten (nur LK)

Erarbeite dir die Eigenschaften von Potenzfunktionen mit negativem Exponenten auf den Seiten 50 - 52. Du kannst für die Visualisierung der Verschiebung und Streckung hier gut GeoGebra verwenden.