Das Heronverfahren ist ein Verfahren zur Berechnung von Quadratwurzeln. Wollen wir z.B. die Wurzel von 50 berechnen, starten wir mit einem Rechteck mit einem Flächeninhalt von 50. Dieses Rechteck Überführen wir mit dem Heronverfahren in ein Quadrat. Die Seitenlänge eines solchen Quadrates ist dann $\sqrt{50}$. Das folgende Video veranschaulicht diesen Prozess:
Hier zeigt sich nach 8 Berechnungsschritten, dass $\sqrt{50}\approx 7.071067811865475$ ergibt.
Doch wie funktioniert das Verfahren? Wir verfolgen das Beispiel von oben rechnerisch.
Gesucht: $\sqrt{50}$
Start: Wir starten mit einem Rechteck mit den Seitenlängen $a=50$ und $b=1$: 
Diese Rechteck hat (offensichtlich) den Flächeninhalt $A=a\cdot b=50$.
1. Schritt: Wir berechnen die Seitenlängen neu, und zwar indem wir zunächst den Mittelwert aus beiden Seitenlängen bilden. Dieser Mittelwert wird unsere neue Seitenlänge $a$:
$$a=\frac{a+b}{2}=\frac{50+1}{2}=\frac{51}{2}=25,5$$
Um sicherzugehen, dass unser Rechteck nach diesem Schritt immer noch den gleichen Flächeninhalt $A=50$ hat, müssen wir die neue Seitenlänge $b$ wie folgt berechnen:
$$b=\frac{50}{a}=\frac{50}{25,5}\approx 1,96$$
Somit sieht unser Recheck nun so aus:

2. Schritt: Wir wiederholen das Verfahren mit den neu berechneten Werten:
$$a=\frac{a+b}{2}=\frac{25,5+1,96}{2}\approx 13,73$$ $$b=\frac{50}{a}=\frac{50}{13,73}\approx 3,64$$

3. Schritt: Wir wiederholen das Verfahren erneut:
$$a=\frac{a+b}{2}=\frac{13,73+3,64}{2}\approx 8,69$$ $$b=\frac{50}{a}=\frac{50}{8,69}\approx 5,76$$

4. Schritt: Und so weiter …
Am Ende ergibt sich diese Tabelle:
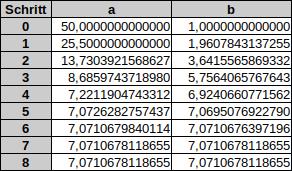
Wie wir sehen, ändern sich die Seitenlängen schon nach dem 7. Schritt nicht mehr. Somit ergibt sich als Lösung:
$$\sqrt{50}=7,0710678118655$$
Berechne mit dem Heron-Verfahren die folgenden Wurzeln:
a) $\sqrt{20}$
b) $\sqrt{9}$
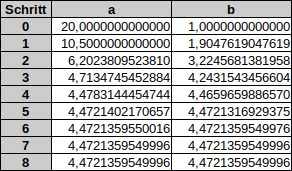
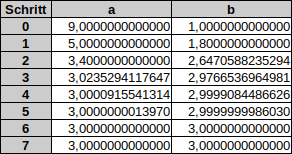
Natürlich können Taschenrechner und Computer das viel schneller und zuverlässiger als wir Menschen. Deswegen lernen wir heute, das Heronverfahren mit Excel zu programmieren. Die so entstandene Excel-Datei können wir einfach verwenden, um Wurzeln auszurechnen:
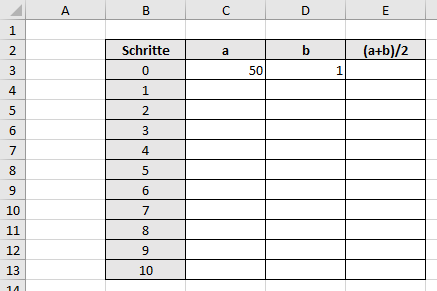
a) Öffne Excel und erstelle eine leere Arbeitsmappe.
b) Erstelle die Tabelle rechts. Achte darauf, dass die Überschriften in den gleichen Zellen stehen wie im Bild!
- "Schritt" in Zelle
B2 - "a" in Zelle
C2 - "b" in Zelle
D2 - "(a+b)/2" in Zelle
E2
a) Trage als Startwerte für $a=50$ in Zelle C3 und für $b=1$ in Zelle D3 ein.
b) Um den Mittelwert zu berechnen, trage in für den Mittelwert in Zelle E3 die Formel =(C3+D3)/2 ein.
a) Trage in Zelle C4 die Formel =E3 ein.
b) Trage in Zelle D4 die Formel =$C$3/C4 ein. Wichtig Die Dollarzeichen $ hier benötigen wir, da die Zelle C3 hier "festgehalten werden soll. Was das bedeutet, sehen wir im nächsten Schritt.
a)
b)
a) Markiere die Zelle E3 und ziehe sie an dem kleinen schwarzen Kästchen eine Zeile nach unten.
b) Markiere die Zellen C4 bis E4 und ziehe sie an dem kleinen schwarzen Kästchen bis ganz nach unten. In Zelle D5 steht nun eine andere Formel wie in Zelle D4, nämlich =$C$3/C5. Hier hat sich die hintere Zelle von C4 zu C5 verändert, die vordere ist aber mit $C$3 gleich geblieben. Hätten wir die Dollarzeichen $ weggelassen, so hätte sich diese Zelle zu C4 verändert. Das wäre aber falsch, da wir dann nicht mehr durch den gesuchten Flächeninhalt teilen würden!
a) Speichere deine Arbeitsmappe unter dem Namen "Heronverfahren.xlsx" und sende sie dir selbst und Herrn Weber per Mail.
b) Berechne die folgenden Wurzeln mit Hilfe der Arbeitsmappe: $\sqrt{20}$, $\sqrt{9}$, $\sqrt{121}$, $\sqrt{5}$, …

