 Martin, Sven, Nadja, Paula und Sarah möchten zusammen einen Urlaub in Flensburg machen, da sie so alle mit einem Auto fahren können. Sie wohnen allerdings alle in unterschiedlichen Städten. Martin kommt aus Neu-Anspach, Sven aus Kassel, Nadja aus Göttingen, Paula aus Hannover und Sarah aus Hamburg. Bei der Planung der Reise kommt folgendes Gespräch zustande:
Martin, Sven, Nadja, Paula und Sarah möchten zusammen einen Urlaub in Flensburg machen, da sie so alle mit einem Auto fahren können. Sie wohnen allerdings alle in unterschiedlichen Städten. Martin kommt aus Neu-Anspach, Sven aus Kassel, Nadja aus Göttingen, Paula aus Hannover und Sarah aus Hamburg. Bei der Planung der Reise kommt folgendes Gespräch zustande:
- Martin: Wie funktioniert so ein Routenplaner eigentlich?
- Sven: Da gibt man zwei Orte ein und der Routenplaner berechnet, welche Strecke am Besten ist und wie lange man dafür braucht.
- Nadja: Da kann man sogar die Art des Fahrzeugs bestimmen und angeben wie der aktuelle Tachostand ist.
- Paula: Dann können wir ja planen, wann wir jeden einzelnen abholen können?
- Sarah: Aber woher weiß der Routenplaner vor der Fahrt, wann man ankommt? Der weiß doch gar nicht, wann man schnell und wann man langsam fährt, und lauter solcher Sachen?
- Martin: Aber wir können doch planen, wenn wir wissen, dass meine Durchschnittsgeschwindigkeit auf der Autobahn 120 km/h ist, oder nicht?
Im Folgenden wird es nun darum gehen, die Planung der Freunde zu unterstützen. Zunächst muss geklärt werden, wann Martin seien Freunde abholen kann.
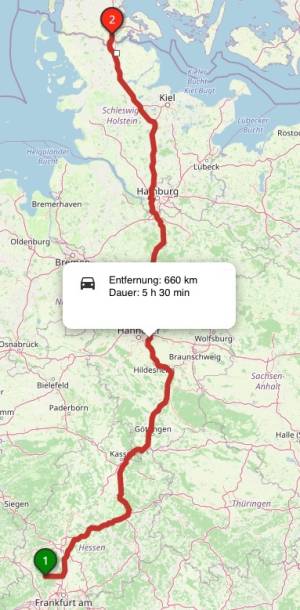
Von der letzten Tour weiß Martin, dass er in 2 Stunden bei Nadja in Göttingen ist. Aus dem Routenplaner wissen sie, dass sie nach Flensburg 5 Stunden und 30 Minuten brauchen. Berechne die fehlenden Zeiten, damit Sven, Paula und Sarah wissen, wann sie jeweils abgeholt werden.
| Stadt | Strecke | Zeit |
|---|---|---|
| Neu-Anspach (Martin) | 0 km | 0 h |
| Kassel (Sven) | 180 km | |
| Göttingen (Nadja) | 240 km | 2 h |
| Hannover (Paula) | 360 km | |
| Hamburg (Sarah) | 480 km | |
| Flensburg | 660 km | 5 h 30 min |
Neben der Tabelle kann ein Graph eine sehr gute Möglichkeit sein, sich Zuordnungen wie die der Fahrzeiten darzustellen. Trage die Punkte aus der Tabelle in das Koordinatensystem ein und verbinde alle zu einer Geraden.

Neben Tabelle und Graph kann man diesen Zusammenhang auch mit der Gleichung
$$y = 120x$$
beschreiben. Hierbei ist…
- …$y$ die gefahrene Strecke
- …$x$ die vergangene Zeit.

Proportionale Zuordnungen können wir auf drei Arten darstellen: als Wertetabelle, Gleichung und Graph. Sie stellen jeweils die gleiche proportionale Zuordnung dar, lediglich die Darstellung ist eine andere.

Wie lange dauert die Strecke nach Flensburg, wenn Martin statt 120km/h nur 60 km/h fahren darf?
| Stadt | Strecke | Zeit |
|---|---|---|
| Neu-Anspach (Martin) | 0 km | 0 h |
| Kassel (Sven) | 180 km | |
| Göttingen (Nadja) | 240 km | |
| Hannover (Paula) | 360 km | |
| Hamburg (Sarah) | 480 km | |
| Flensburg | 660 km |
Die Werte in den folgenden Tabellen sind Voraussetzungen eines Routenplaners. Es handelt sich in jeder Tabelle um eine proportionalen Zusammenhang.
Zur Erinnerung: Eine wichtige Eigenschaft des proportionalen Zusammenhangs ist, dass man bei 0 h genau 0 km gefahren ist. Man sagt, dass der Zeit 0 h die Strecke 0 km zugeordnet wird.
a) Ergänze folgende Tabellen.
| Zeit in h | Strecke in km |
|---|---|
| 0 | |
| 1 | |
| 2 | 48 |
| 10 | |
| 15 |
| Zeit in h | Strecke in km |
|---|---|
| 0 | |
| 1 | |
| 1,5 | 9 |
| 2,25 | |
| 3 |
| Zeit in h | Strecke in km |
|---|---|
| 15 | |
| 1 | 30 |
| 45 | |
| 75 | |
| 135 |
b) Zeichne zu jeder Tabelle den Graphen. Hierbei kann dir das Video unten helfen!
c) Beschreibe deine Graphen und nenne die Gemeinsamkeiten der Graphen.
d) Ordne den Tabellen jeweils eine der Gleichungen zu (eine Gleichung passt nicht):
- $y=2x$
- $y=6x$
- $y=9x$
- $y=30x$
Fülle anhand der gegebenen Graphen die Wertetabellen aus.

| $x$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| $y$ |

| $x$ | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| $y$ |

| $x$ | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| $y$ |
Werden die Werte einer proportionalen Zuordnung oder Funktion größer, je größer das $x$ wird, so spricht man von einer steigenden Zuordnung oder Funktion. Graphen steigender proportionaler Funktionen könnten z.B. wie folgt aussehen:

Die Gleichung einer steigenden proportionalen Zuordnung hat einen positiven Faktor vor dem $x$. Beispiele wären:
- $y = 0,5x$
- $y = x$
- $y = 3x$
- $y = 42x$
- …
Werden die Werte einer proportionalen Zuordnung oder Funktion kleiner, je größer das $x$ wird, so spricht man von einer fallenden Zuordnung oder Funktion. Graphen fallender proportionaler Funktionen könnten z.B. wie folgt aussehen:

Die Gleichung einer steigenden proportionalen Zuordnung hat einen positiven Faktor vor dem $x$. Beispiele wären:
- $y = -0,5x$
- $y = -x$
- $y = -3x$
- $y = -42x$
- …
Als Bild kann man sich hier ein Auto vorstellen, das von links nach rechts fährt. Wenn dieses bergauf fährt, steigt der Graph, fährt es bergab, fällt der Graph.
Auto von Freepik auf www.flaticon.com
Hannes behauptet: "Wenn ich wissen möchte, wie schnell ein Fahrzeug gefahren ist, dann reicht es, in der Tabelle die gefahrene Strecke nach einer Stunde zu bestimmen."
Was sagst du zu Hannes Aussage? Begründe deine Überlegungen.
