Dies ist eine alte Version des Dokuments!

Lektion 2: Grundlegende Operatoren

kartesisches Produkt, Join

Projektion

Die Projektion kann auch Attributbeschränkung genannt werden. Sie extrahiert einzelne Attribute aus der ursprünglichen Attributmenge und ist somit als eine Art Selektion auf Spaltenebene zu verstehen, das heißt, die Projektion blendet Spalten aus. Wenn $\beta$ die Attributliste ist, schreibt man $\pi_\beta(R)$. $\beta$ heißt auch Projektionsliste. Duplikate in der Ergebnisrelation werden eliminiert.

Definition

Sei $R$ eine Relation über $\{A_1, ..., A_k\}$ und $\beta \subseteq \{A_1, ..., A_k\}$.

$\pi_\beta(R):=\{t_\beta|t\in R\}$

Hierbei heißt $t_\beta := (\beta)$, das heißt, die Tupel erhalten nur die Attribute aus der Attributliste $\beta$.

Beispiel

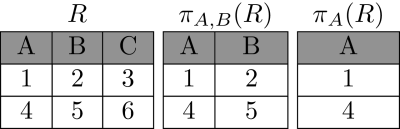
SQL

$\pi_{A,B}(R)$

SELECT A, B
FROM R;

$\pi_{A}(R)$

SELECT A
FROM R;

Selektion

Bei der Selektion kann man mit einem Vergleichsausdruck $\gamma$ (Prädikat) eine Auswahl von Tupeln festlegen, die in die Ergebnismenge aufgenommen werden sollen. Es werden also Tupel ("Zeilen") ausgeblendet. Man schreibt $\sigma_{\gamma}(R)$. $\gamma$ heißt dann Selektionsbedingung.

Definition

Sei $R$ eine Relation.

$\sigma_{\gamma}(R):=\{t|t\in R\wedge \gamma(t)\}$

$\gamma(t)$ bezeichnet dabei eine Formel. Diese kann bestehen aus:

Konstantenselektionen, z.B. $A~=~\text{"Test"}$ oder $C~\leq~12$
Attributselektionen, z.B. $A > C$
Verknüpfungen mit logischen Prädikaten, z.B. $\neg(A~\geq~5~\wedge~B~=~\text{"Test"})$

Beispiel

SQL

$\sigma_{A=1}(R)$

SELECT *
FROM R
WHERE A=1;

$\sigma_{C>6}(R)$

SELECT *
FROM R
WHERE C>6;