Methoden & Funktionen

Aufgabe 1: Fachkonzepte

Lest das Fachkonzept: Methode und Fachkonzept: Don't Repeat Yourself.

Aufgabe 2: Übung

Aus der letzten Lektion wisst ihr, wie man mit verschachtelten Schleifen z.B. das folgende Bild erzeugt.

Beide Sketche unten erzeugen die gleiche Ausgabe. Vergleicht die beiden Sketche und überlegt, wieso es hier sinnvoll ist, Methoden zu verwenden. Passt dann das zweite Programm so an, dass die Punkte auch die korrekte Größe haben.

void setup() {
  size(200, 200);
}
 
void draw() {
  background(200);
  stroke(255, 0, 0);
  strokeWeight(5);
 
  for (int x = 20; x < width; x += 20) {
    for (int y = 20; y < height; y += 20) {
      point(x, y);
    }    
  }
}

void setup() {
  size(200, 200);
}
 
void draw() {
  background(200);
  stroke(255, 0, 0);
  strokeWeight(5);
 
  for (int x = 20; x < width; x += 20) {
    spalte(x); 
  }
}
 
void spalte(int x) {
  for (int y = 20; y < height; y += 20) {
    punkt(x, y);
  }  
}
 
void punkt(int x, int y) {
  point(x, y);
}

Passt nun das folgende Programm aus der vorherigen Lektion so an, dass auch Methoden verwendet werden:

void setup() {
  size(200, 200);
}
 
void draw() { 
  background(255);
  stroke(255, 0, 0);
  strokeWeight(1);
  rectMode(CENTER);
 
  for (int y = 9; y < height; y += 20) {
    for (int x = 9; x < width; x += 20) {
      for (int d = 18; d > 0; d -= 4) {
        rect(x, y, d, d); 
      }
    }    
  }
}

Aufgabe 3: Eigenes Bild

Programmiert dieses Bild unter der Verwendung von Methoden:

Aufgabe 4: Weiteres Fachkonzept

Lest das Fachkonzepte: Funktion & Return und das Fachkonzept: SoC - Separation of Concerns.

Aufgabe 5:

Funktionen können nicht nur Zahlen als Datentypen haben, sondern z.B. auch Farben. Versuche, das folgende Programm nachzuvollziehen:

void setup() {
  size(300, 300);
}
 
void draw() {
  int bereiche = 3;
  int bereichsGroesse = width / bereiche;
 
  noStroke();
 
  for (int bereich = 0; bereich < bereiche; bereich++) {
    fill(bereichsFarbe(bereich));
 
    rect(bereich * bereichsGroesse, 0, bereichsGroesse, height);
  }
}
 
color bereichsFarbe(int bereich) {
  if (bereich == 0) return #FF0000;
  else if (bereich == 1) return #00FF00;
  else if (bereich == 2) return #0000FF;
 
  return #FFFFFF;
}

Ändere nun das Programm: int bereiche = 5; Was passiert?
Sorge dafür, dass die beiden anderen Bereiche auch eine Farbe bekommen.
Ändere nun das Programm erneut: rect(bereich * bereichsGroesse, 0, bereichsGroesse, bereichsHoehe(bereich));.
- Erstelle eine neue Funktion bereichsHoehe(…), die die Höhe des angegebenen Bereichs ermittelt. Am Ende soll es so aussehen:

Lösung zu Aufgabe 5

void setup() {
  size(300, 300);
}
 
void draw() {
  int bereiche = 5;
  int bereichsGroesse = width / bereiche;
 
  noStroke();
 
  for (int bereich = 0; bereich < bereiche; bereich++) {
    fill(bereichsFarbe(bereich));
 
    rect(bereich * bereichsGroesse, 0, bereichsGroesse, bereichsHoehe(bereich));
  }
}
 
color bereichsFarbe(int bereich) {
  if (bereich == 0) return #FF0000;
  else if (bereich == 1) return #00FF00;
  else if (bereich == 2) return #0000FF;
  else if (bereich == 3) return #00FFFF;
  else if (bereich == 4) return #FF00FF;
 
  return #FFFFFF;
}
 
int bereichsHoehe(int bereich) {
  return height - bereich * 25;
}

Aufgabe 6: Funktionsplotter

Betrachten wir das folgende Programm, dass einfache Funktionen zeichnen soll:

void setup() {
  size(500, 500);
}
 
void draw() {
  background(255);
 
  // Koordinaten-Ursprung zur Mitte des Fensters verschieben
  translate(width / 2, height / 2);
 
  zeichneKoordinatenGitter();
 
  strokeWeight(4);
 
  for (int x = -width / 2; x <= width / 2; x++) {
    stroke(255, 0, 0);
    point(x, -f(x));
 
    stroke(0, 255, 0);
    point(x, -g(x));
 
    stroke(0, 0, 255);
    point(x, -h(x));
  }
}

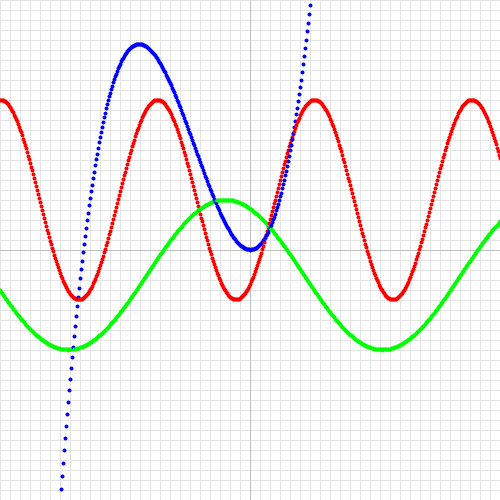
void zeichneKoordinatenGitter() {…}

void zeichneKoordinatenGitter() {
  strokeWeight(1);
  stroke(228);
 
  for (int x = 10; x <= width / 2; x += 10) {
    line(x, -height/2, x, height/2);
    line(-x, -height/2, -x, height/2);
  }
 
  for (int y = 10; y <= height / 2; y += 10) {
    line(-width/2, y, width/2, y);
    line(-width/2, -y, width/2, -y);
  }
 
  stroke(192);  
  line(0, -height/2, 0, height/2);
  line(-width/2, 0, width/2, 0);
}

Wie wir sehen, gibt es eine Methode, die ein Koordinatengitter zeichnet. Außerdem werden die drei Funktionen $f(x)$, $g(x)$ und $h(x)$ gezeichnet. Diese sind mathematisch wie folgt definiert:

$f(x)=100\cdot sin(\frac{x-25}{25})+50$
$g(x)=75\cdot cos(\frac{x+25}{50})-25$
$h(x)=0.0003x^3+0.05x^2$

Wichtig! Da Processing positive Werte "nach unten" zeichnet, müssen die Funktionswerte negiert werden, um die Funktionen auf die für uns aus der Mathematik gewöhnliche Art und Weise zu zeichnen. Deswegen das Minus in point(x, -f(x));.

Erweitere den Funktionsplotter, indem du die folgenden Funktionen passend zu den mathematischen Definitionen oben ergänzt. Nutze dazu die folgende Vorlage:

float f(float x) {
  return 0 * x;
}

Lösung zu Aufgabe 6

float f(float x) {
  return 100 * sin((x - 25) / 25) + 50;
}
 
float g(float x) {
  return 75 * cos((x + 25) / 50) - 25;
}
 
float h(float x) {
  return 0.0003 * x*x*x + 0.05 * x*x;
}

Aufgabe 7: Erweitere den Funktionsplotter

Erweitere den Funktionsplotter aus Aufgabe 6:

Der Plotter soll standardmäßig ein leeres Koordinatensystem anzeigen
Wenn man die Taste f drückt, soll die Funktion $f(x)$ angezeigt werden, wenn man g drückt, dann $g(x)$ und wenn man h drückt, dann $h(x)$.
Füge mindestens 2 eigene Funktionen $i(x),k(x),\ldots$ hinzu. Schau dir dazu z.B. die folgenden Funktionen aus Processing an: exp(x), log(x), pow(a, x), sqrt(n), sin(x), cos(n), tan(n)
Wenn man die Taste a drückt, sollen alle Funktionen gleichzeitig angezeigt werden.

Lösung zu Aufgabe 7

void setup() {
  size(500, 500);
 
  background(255);
  translate(width / 2, height / 2); 
  zeichneKoordinatenGitter();
}
 
void draw() {}
 
void keyPressed() {
  background(255);
  translate(width / 2, height / 2); 
  zeichneKoordinatenGitter();
 
  strokeWeight(4);
  println(key);
 
  if (key == 'f' || key == 'a') { 
    for (int x = -width / 2; x <= width / 2; x++) {
      stroke(255, 0, 0);
      point(x, -f(x));
    }
  }
 
  if (key == 'g' || key == 'a') { 
    for (int x = -width / 2; x <= width / 2; x++) {
      stroke(0, 255, 0);
      point(x, -g(x));
    }
  }
 
  if (key == 'h' || key == 'a') { 
    for (int x = -width / 2; x <= width / 2; x++) {
      stroke(0, 0, 255);
      point(x, -h(x));
    }
  }
 
  if (key == 'i' || key == 'a') { 
    for (int x = -width / 2; x <= width / 2; x++) {
      stroke(255, 255, 0);
      point(x, -i(x));
    }
  }
 
  if (key == 'k' || key == 'a') { 
    for (int x = -width / 2; x <= width / 2; x++) {
      stroke(255, 0, 255);
      point(x, -k(x));
    }
  }
}
 
void zeichneKoordinatenGitter() {
  strokeWeight(1);
  stroke(228);
 
  for (int x = 10; x <= width / 2; x += 10) {
    line(x, -height/2, x, height/2);
    line(-x, -height/2, -x, height/2);
  }
 
  for (int y = 10; y <= height / 2; y += 10) {
    line(-width/2, y, width/2, y);
    line(-width/2, -y, width/2, -y);
  }
 
  stroke(192);  
  line(0, -height/2, 0, height/2);
  line(-width/2, 0, width/2, 0);
}
 
float f(float x) {
  return 100 * sin((x - 25) / 25) + 50;
}
 
float g(float x) {
  return 75 * cos((x + 25) / 50) - 25;
}
 
float h(float x) {
  return 0.0003 * x*x*x + 0.05 * x*x;
}
 
float i(float x) {
  return 0.0003 * pow(x/10, 5) - 0.05 * pow(x/10, 3);
}
 
float k(float x) {
  return 10 * sqrt(abs(x));
}