In der letzten Lektion haben wir wiederholt, was proportionale Zuordnungen sind. In dieser Lektion werden wir lernen, was eine lineare Funktion ist und was diese von einer proportionalen Zuordnung unterscheidet.
Es gibt Situationen, in denen sich eine Größe proportional ändert, aber ein fester Wert wie z.B. eine Grundgebühr oder ein Anfangsbestand zusätzlich berücksichtigt werden muss.
Du willst auf dem Jahrmarkt Dosenwerfen. Hier musst du als Grundgebühr 2€ und pro Wurf 0,20€ bezahlen. Stelle eine Wertetabelle auf und zeichne den zugehörigen Graphen. Stelle anschließend eine Funktionsgleichung auf.
Lösung:
| x=Anzahl der Würfe | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
|---|---|---|---|---|---|---|---|---|
| y=Kosten in € | 2 | 2,20 | 2,40 | 2,60 | 2,80 | 3,00 | 3,20 | … |
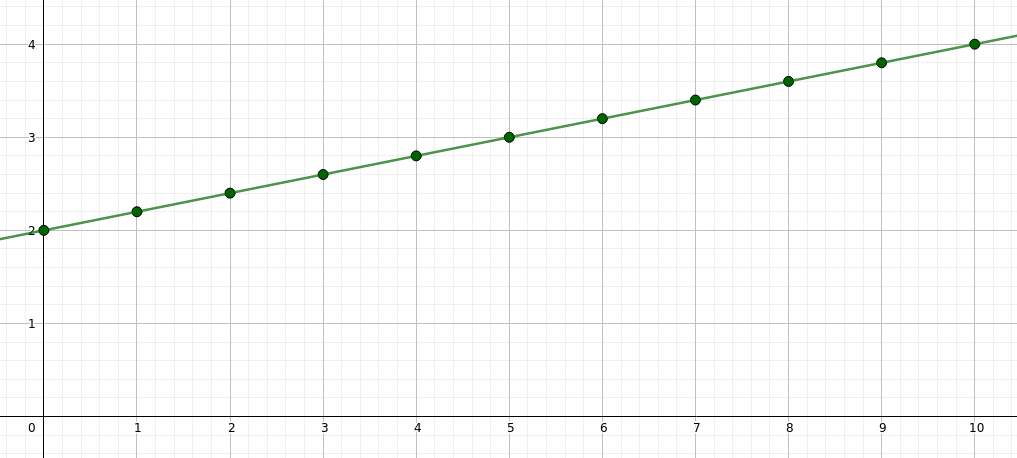
Die Funktionsgleichung lautet $y=0,2\cdot x + 2$, da der Zusammenhang proportional ist (Pro Wurf bezahlt man 0,20€). Dazu addiert man noch die Grundgebühr von 2€.
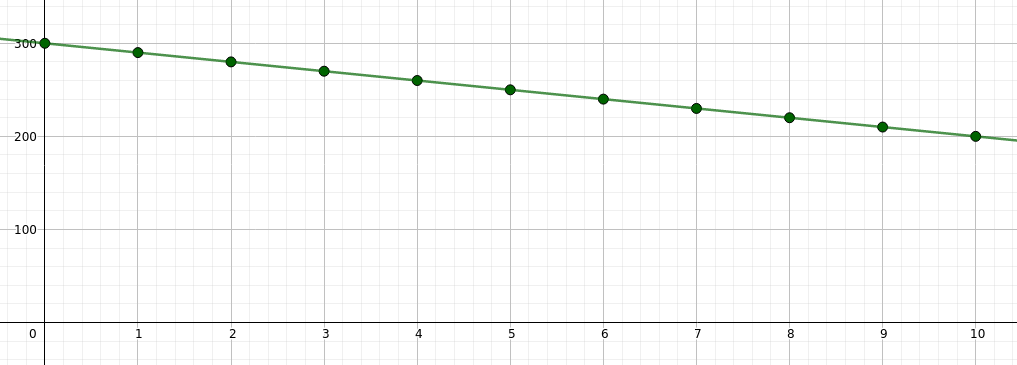
Eine Regentonne enthält 300l Wasser. Wenn man den Wasserhahn aufdreht, fließen pro Minute 10l heraus. Stelle eine Wertetabelle auf und zeichne den zugehörigen Graphen. Stelle anschließend eine Funktionsgleichung auf.
Lösung:
| x=Anzahl der Minuten | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
|---|---|---|---|---|---|---|---|---|
| y=Wassermenge in Litern | 300 | 290 | 280 | 270 | 260 | 250 | 240 | … |
Die Funktionsgleichung lautet $y=300-10x$, da der Zusammenhang proportional ist (pro Minute verliert die Tonne 10 Liter Wasser). Dazu addiert man noch die Anfangsmenge von 300l.
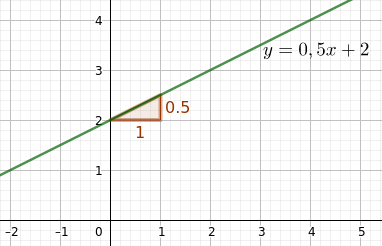
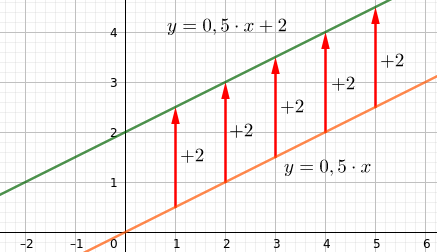
Die lineare Funktion $y=0,5x+2$ unterscheidet sich von der proportionalen Zuordnung $y=0,5x$ nur durch die Zahl $2$, die zu jedem Funktionswert addiert wird.
Der Graph zu $y=0,5x+2$ entsteht durch eine Verschiebung des Graphen zu $y=0,5x$ um 2 Einheiten nach oben.
Der zugehörige Graph ist eine Gerade mit der Steigung $m$, die die y-Achse im Punkt $(0 |b)$ schneidet.
$b$ wird als y-Achsenabschnitt und $m$ als Steigung bezeichnet.
- Übernehmt den Merksatz oben ins Heft.
- Schaut euch bei Bedarf die Videos unten an. Sie helfen euch bei den folgenden Aufgaben:
- Bearbeite im Buch auf S. 117 die drei Beispiele.
- Bearbeite anschließend auf S. 118 die Aufgaben 1, 3, 4, 6 und auf S. 119 die Aufgaben 9 und 10.